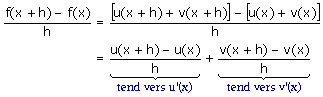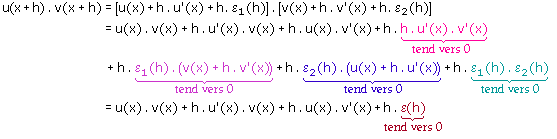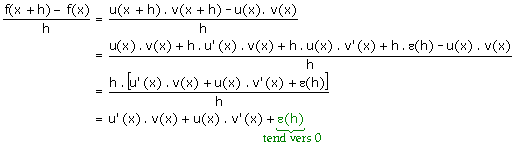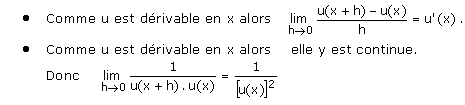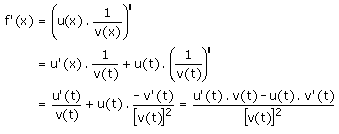Dérivée du produit de deux
fonctions retour.
x est un réel fixé.
u
et v sont deux fonctions dérivables
en x. On appelle f leur produit.
Ainsi pour tout t :
f(t)
= u(t) . v(t)
Pour déterminer si f
est dérivable en x, nous devons étudier la limite lorsque h tend vers
0 du quotient 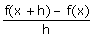 . .
Commenc¸ons par exploiter les
dérivabilités de u et v
au point x :
- Comme u
est dérivable en x alors il
existe une fonction e1 telle que :
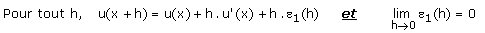
- Comme v
est dérivable en x alors il existe une fonction e2
telle que :
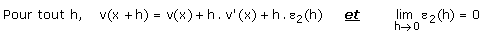
Avant de nous intéresser au quotient 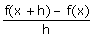 ,
simplifions l'écriture de f(x + h) : ,
simplifions l'écriture de f(x + h) :
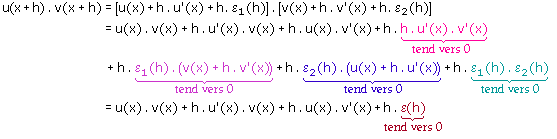
Pour tout h non nul, on peut écrire
que :
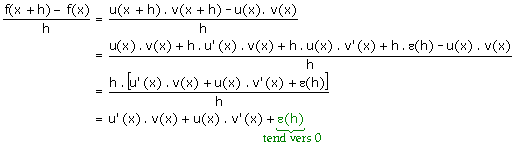
Donc lorsque la limite
lorsque h tend vers 0 du quotient 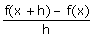 est égale à
est égale à
u'(x) . v(x) + u(x) . v'(x).
| Conclusion:si
deux fonctions u et v
sont dérivables en x alors leur produit est également
dérivable en ce point. De plus :
(u
. v)' (x)
= u'(x) . v(x)
+ u(x) . v'(x) |
|
Une méthode plus astucieuse:
Il existe une autre méthode pour démontrer que le quotient 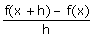 admet une limite lorsque h tend vers 0. Il suffit de
modifier l'écriture.
admet une limite lorsque h tend vers 0. Il suffit de
modifier l'écriture.

Après, il ne reste
plus qu'à conclure... |
|